CSS Statistics Past Paper 2016
PART-II (Subjective) 80 Marks
Attempt ONLY FOUR Questions from PART-II by selecting TWO questions from EACH SECTION. (20×4)
PART-II
SECTION – A
Q. No. 2. (a) Describe the importance of skewness and kurtosis. Also give the major characteristics of a frequency distribution.
(b) The fourth mean moment of a symmetrical distribution is 243. What would be the value of the standard deviation in order that the distribution may be mesokurtic?
(c) Find the arithmetic, geometric, and harmonic means of the series:
1, 2, 4, 8, 16,…, 2n
Q. No. 3. (a) Describe the importance of hypergeometric probability distributions. In reality, where can we use it?
(b) If N becomes indefinitely large, the hypergeometric probability distribution tends to the binomial probability distribution. Prove it.
(c) A continuous r.v. X has the p.d.f., given by
f(x) = w(2 − x)(5 − x) for 2 ≤ x ≤ 5, and 0 otherwise.
Find the value of w, mean, and variance. What are the values of the mode and median of the distribution of X?
Q. No. 4. (a) What are the assumptions made in linear regression? Give the important uses of regression analysis.
(b) Differentiate between correlation and regression with two real-life examples.
(c) The following measurements show the respective heights in inches of ten fathers (X) and their eldest sons (Y).

(i) Find the regression line of Y on X.
(ii) Estimate Y for X = 70 inches.
(iii) Test the significance of the population regression coefficient βyx.
(iv) Calculate 95% confidence limits for βyx.
(v) Test the significance of the intercept of the line Y on X.
(vi) Find the regression line of X on Y.
Q. No. 5. (a) What are the steps involved in any nonparametric test of hypothesis?
(b) Describe briefly Kolmogorov-Smirnov test of goodness of fit in case of one and two samples.
(c) Following is a sequence of heads (H) and tails (T) in the tossing of a coin 14 times, HTTHHHTHTTHHTH. Test whether the heads and tails occur in random order. [Given: For α = 5%, rL =2, ru=12].
SECTION – B
Q. No. 6. (a) Describe the importance of sampling. Also, discuss sampling with and without replacement.
(b) What steps should be kept in mind to determine the sample size?
(c) A population consists of N = 7 numbers, 1, 1, 2, 3, 4, 4, 5.
Draw all possible samples of size n = 3 without replacement from this population and find the sample properties of odd numbers in the samples. Construct the sampling distribution of sample proportion and verify:
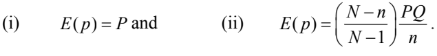
Q. No. 7.
(a) Differentiate between simple and composite hypotheses. Also, discuss the role of the “Test of significance.”
(b) In a random sample of 500 men from Lahore city, 300 are found to be smokers. In a sample of 1000 men from Karachi city, 550 are smokers. Do the data indicate that the two cities are significantly different with respect to the prevalence of smoking among men?
(c) Test the hypothesis that the variances of three populations are equal at α = 5%.

Q. No. 8.
(a) What is meant by Analysis of Variance and degrees of freedom? What are the assumptions underlying a one-way analysis of variance?
(b) Given the following information:
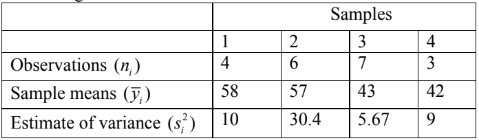
Construct an analysis of variance table and test the hypothesis that the population means are equal at α = 5%.
(c) Describe the role of Pakistan Bureau of Statistics and NADRA.
